LA ELIPSE Y
LA HIPÉRBOLA
-Conceptos y
elementos de la elipse
Una elipse se define como el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Su representación gráfica es:
Elementos
de la elipse:
- Focos: son los puntos fijos F y F’.
- Eje focal: es la recta que pasa por
los focos.
- Eje secundario: es la mediatriz del
segmento FF’.
- Centro: es el punto de intersección de
los ejes.
- Radios vectores: son los segmentos
que van desde un punto de la elipse a los focos PF y PF’
- Distancia focal: es el segmento de
longitud 2c, c es el valor de la semidistancia focal.
- Vértices: son los puntos de intersección
de la elipse con los ejes A, A’ y B, B’.
- Eje mayor: es el segmento de longitud
2a, a es el valor del semieje mayor.
- Eje menor: es el segmento de
longitud 2b, b es el valor del semieje menor.
- Ejes de simetría: son las rectas que
contienen al eje mayor o al eje menor.
- Centro de simetría: coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
¿Cómo graficarla?
Una elipse horizontal con centro en
el origen tiene una excentricidad![]()
y las coordenadas de sus focos son![]() . Hallar la ecuación de dicha elipse y dibuje su gráfica.
. Hallar la ecuación de dicha elipse y dibuje su gráfica.
Solución:
Inicialmente conviene graficar los
datos del enunciado, en este caso los focos y el centro, los cuales se muestran
en la figura.
Recordando que la distancia del centro de una elipse a cualquiera de los
focos es c, se tiene entonces que![]() . Además, como el centro está en el origen, se obtiene que
. Además, como el centro está en el origen, se obtiene que![]() .
.
Por otra parte, sabiendo la excentricidad que está dada por la relación
Conociendo los valores de e y de c se obtiene que
De donde
Conociendo los valores de las constantes a=4 y c=3.464 se calcula que b es igual a:
Por lo tanto, su ecuación es
La gráfica se muestra en la figura
-Conceptos y elementos de la hipérbola
Elementos de la Hipérbola
- Focos: son los puntos fijos F y F’.
- Eje principal o real: es la recta
que pasa por los focos.
- Eje secundario o imaginario: es la
mediatriz del segmento FF’
- Centro: es el punto de intersección de
los ejes.
- Vértices: los puntos A y A’ son los
puntos de intersección de la hipérbola con el eje focal. Los puntos B y B’ se obtiene
como intersección del eje imaginario con la circunferencia que tiene por centro
uno de los vértices y de radio c.
- Radios vectores: son las rectas que
contienen al eje real o al eje imaginario.
- Distancia focal: es el segmento
 de la longitud 2c.
de la longitud 2c. - Eje mayor: es el segmento
 de longitud 2a.
de longitud 2a. - Eje menor: es el segmento
 de longitud 2b.
de longitud 2b. - Ejes de simetría: son las rectas que
contienen al eje real o al eje imaginario.
- Asíntotas: son las rectas de ecuaciones
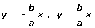
- Relación entre los semiejes:

¿Cómo graficarla?
Al graficar
una hipérbola, puedes pensar en ella como una mezcla de dos parábolas – cada una
con una perfecta imagen espectacular de la otra y cada una abriéndose una a la
otra. La definición matemática de una hipérbole es el conjunto de todos los puntos
donde la diferencia en la distancia entre dos puntos fijos (llamados focos) es
constante. Las hipérbolas se presentan en dos tipos: horizontales y verticales.
· Debido
a que esta ecuación es para una hipérbola vertical, se encuentra que el centro
(h, v) de esta hipérbola es (-1,3). Recuerde, los signos de los números dentro del
paréntesis son opuestos a los de las coordenas del centro. También recuerde que
h está dentro de los paréntesis con x y v no cambian de lugar. Las h y v
siempre permanecen fieles a sus respectivas variables, x e y.
· Desde
el centro en el Paso 1, encuentra los ejes transversal y conjugado, sube y baja
el eje transversal a una distancia de 4 (porque 42 está por debajo de y), y
luego va a la derecha e izquierda 3 (porque 32 está por debajo de x). ¡Pero no
conecte los puntos para obtener una elipse! Hasta ahora, los pasos para dibujar
una hipérbola eran exactamente los mismos que para dibujar una elipse, pero aquí
es donde se diferencian: los puntos que has marcado como a son tus vértices.
· Utiliza
estos puntos para dibujar un rectángulo que te ayudara a guiar la forma de tu hipérbola,
ya que subiste y bajaste 4, la altura de tu rectángulo es 8; yendo a la izquierda
y a la derecha 3 te da un ancho de 6.
· Dibuja
líneas diagonales a través del centro y las esquinas del rectángulo que se
extienden más allá del rectángulo, este paso te da dos líneas que serán tus
asíntotas.
· A
partir de cada vértice por separado, dibuje las curvas que se aproximan a las
asíntotas cuando mas lejos se encuentren de los vértices de la curva. El gráfico
se acerca a las asíntotas, pero nunca los toca, creando un rectángulo para
graficar una hipérbola con asíntotas.






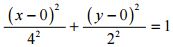




Comentarios
Publicar un comentario